LaTeX3 Quick Reference Guide

As I am getting more and more familiar with LaTeX, my personal need of writing complicated LaTeX packages continue to increase. However, I am totally blown away by the complexity of expansion control in tradition LaTeX. Fortunately, the LaTeX3 project provides a way to write large scale LaTeX programs with much simpler expansion control and more systemic naming conventions. This post serves as a quick guide to introduce one to LaTeX3.

LaTeX is turing complete! If you know how to control expansions, you can pretty much do everything with LaTeX (tough the efficiency is awful).

Why LaTeX3?

• To achieve the separation of function and variables
• To control the expansion of function parameters easily
• To handle data structures such as queues, sets, stacks, lists, etc.
• To separate public and private code systematically
• To encapsulate related macros and variables into modules

Personally, I want to use LaTeX3 because it provides better mechanism of controlling parameter expansion. In old LaTeX, usually the following macros are provided for expansion control:

• \edef, \noexpand
• \expandafter

However, \edef will expand everything recursive: it is very difficult to expand a macro only once. To expand something by a given amount of times, one needs to fall back to \expandafter, which is extremely obscure to use. Check out the example below:

\documentclass{article}
\begin{document}

\def\x#1#2#3#4{%
  \def\arga{#2}%
  \def\argb{#3}%
  \def\argc{#4}%
  \expandafter\expandafter\expandafter\expandafter\expandafter\expandafter\expandafter#1%
    \expandafter\expandafter\expandafter\expandafter\expandafter\expandafter\expandafter
      {\expandafter\expandafter\expandafter\arga\expandafter\expandafter\expandafter}%
        \expandafter\expandafter\expandafter{\expandafter\argb\expandafter}\expandafter
          {\argc}}

\def\y#1#2#3{\detokenize{#1#2#3}}

\x\y{arg1}{arg2}{arg3}

\end{document}

It is very difficult to understand programming with \expandafter correctly. It is suggested that reversing the expansion of \(n\) TeX tokens, the \(i\)th token has to be preceded with \(2^{n-i} - i\) \expandafters. There is clearly something wrong with it since this programming convention drastically reduce readability and maintainability. Therefore, I decide to turn to more advanced expansion controls provided by LaTeX3. If you want to know more about \expandafter, please refer to resources.

LaTeX3 naming convention

Instead of using @ for internal macros (as in traditional TeX), LaTeX3 mainly uses _ and : for naming.

Remarks

• Only letters are allowed in names
• All symbols must be declared before use

Variables

For more details about <type>, see data types.

• Template: \<scope>_<module>_<description>_<type>
• <scope>: l=local; g=global; c=constant
• <module>: the name of the module
• <description>: description of the variable

Examples

• \l_mymodule_tmpa_box
• \g_mymodule_tmpb_int

Functions

For more details about <arg-spec>, see function argument specs.

• Template: \<module>_<description>:<arg-spec>
• <module>: the name of the module
• <description>: description of the variable

Examples

• \seq_push:Nn
• \if_cs_exist:N

Private symbols

The naming convention for public and private symbols are different.

• Public symbols follow standard naming conventions.
• Private functions start with __.
• Private variables have two underscores after <scope>.

Private symbol examples

• \__mymodule_foo:nnn
• \l__mymodule_foo_int

Using @@ and l3docstrip to mark private code

To avoid typing the module name repeatedly in private code sections, the l3docstrip programs introduces the following syntax:

%%<@@=(module)>

Afterwards, the @@ in private code sections will be substituted with module name automatically. For example,

% \begin{macrocode}
\cs_new:Npn \@@_function:n #1
...
\tl_new:N \l_@@_my_tl
% \end{macrocode}

will be converted to

\cs_new:Npn \__foo_function:n #1
...
\tl_new:N \l__foo_my_tl

Data types

• Standard types
  • bool: either true or false
  • fp: floating point values
  • int: integer
• Boxes
  • box: box register
  • coffin: a “box with handles”
• Lists (Sequences)
  • clist: comma seperated list
  • prop: property list
  • seq: sequence (a data type used to implement lists and stacks)
  • tl: token list variables (placeholders for token lists)
  • str: TeX strings (a special case of tl in which all characters have category “other” (catcode 12), other than spaces which are category “space” (category 10))
• Length (wiki)
  • dim: “rigid” lengths
  • muskip: math mode “rubber” lengths
  • skip: “rubber lengths”
• I/O Stream (example)
  • ior: input stream
  • iow: output stream

Remarks

• clist is preferred for creating fixed lists inside programs and for handling user input where commans will not occur. On the onther hand, seq can be used to store arbitrary lists of data.

Function argument specifications

Function arguments are specified with a single case-sensitive letter.

• n: unexpanded token or braced token list.
• N: single token (the argument must not be sourrounded by braces)
• p: primitive TeX parameter
• T, F: special cases for n, used for true/false code in conditional commands
• D: do not use (not for normal users)
• w: “weird” arguments: arguments that do not follow any standard rules.

Expansion control

To denote function arguments that need special expansion treatment, the following argument specifications are used:

• c: character string used as a command name

  The argument (a token or braced token list) will be fully expanded and passed as a command name. For example,

  \seq_gpush:cV { g_file_name_seq } \l_tmpa_tl
  

  is equivalent to

  \seq_gpush:NV \g_file_name_seq \l_tmpa_tl
  

</pre></div>

• V: value of variable
• v: value of a register, constructed from a character string used as a command name. This is the combination of V and c.
• x: fully-expanded token or braced token list (like \edef)
• e: fully-expanded token or braced token list which does not require double # tokens.
• f: expanding the first token recursively in a braced token list until the first unexpandable token is found and the rest is left unchanged.
• o: one-level-expanded token or braced token list. If the original argument is a braced token list then only the first token in that list is expanded. In general, using V should be preferred to using o for simple variable retrieval.

Examples

More coding examples can be found in LeetCode (LaTeX) page.

Minimal preamble

To use LaTeX3, one needs to load expl3 package. Despite having the word “experimental” in the name, LaTeX3 is now fairly stable.

\documentclass{article}
\usepackage{expl3}

\begin{document}
test
\end{document}

Expanding a simple argument

Suppose I want to control reuse the optional arguments of a tcbox command which is stored in \boxargs, as it is shown below.

\documentclass{article}

\usepackage[T1]{fontenc}
\usepackage[margin=1.1in]{geometry}
\usepackage{mathptmx}
\usepackage{tcolorbox}
\usepackage{expl3}

\begin{document}

\def\boxargs{title=test, colframe=blue}
\newcommand{\mybox}[1]{\tcbox[\boxargs]{#1}}
\mybox{content}

\end{document}

This code will not work because \boxargs is not expanded properly, which means the following error will occur:

! Package pgfkeys Error: I do not know the key '/tcb/title=test, colframe=blue'
 and I am going to ignore it. Perhaps you misspelled it.

With LaTeX3, we can rewrite the mybox command as follows:

\ExplSyntaxOn

\tl_gset:Nn \g_boxargs_tl {title=test, colframe=blue}
\cs_gset:Npn \mybox_create:nn #1#2 {
\tcbox[#1]{#2}
}
\cs_generate_variant:Nn \mybox_create:nn {Vn}

\cs_gset:Npn \mybox #1 {\mybox_create:Vn \g_boxargs_tl {#1}}

\ExplSyntaxOff


\mybox{test}

Remarks

• The LaTeX3 code segment should be enclosed by \ExplSyntaxOn and \ExplSyntaxOff. It is worth noticing that all white spaces are ignored in between.
• Each type has its corresponding set and new functions. For example, for tl, use \tl_gset and \tl_set to declare new variables.
• Use \cs_gset or \cs_set to declare new macros.
• When a command is first declared, all of its arguments are of type n by default. For example, \mybox_create:nn first has argument types nn. In order to change the first argument to V (expand once), we need to declare a variant \mybox_create:Vn with \cs_generate_variant:Nn.
• An easier (yet less flexible) approach to expand arguments without declaring a variant is to use the \exp_args: series. It has a set of predefined-variants for expanding arguments quickly.

Constructing and calling a command name containing star

For example, we want to call \section*{abc} and \subsection*{abc} by calling another macro \__new_section:nn {section} {abc} and \__new_section:nn {subsection} {abc}. We need to use \exp_last_unbraced:No.

\cs_set:Npn \__new_section:nn #1#2 {
  \cs_set_eq:Nc {\__sec_tmp} {#1}
  \exp_last_unbraced:No \__sec_tmp {*} {#2}
}

Multiplying a length by a floating-point factor

This macro reads a length in #1, multiply it by the factor in #3 and save it in #2.

\cs_generate_variant:Nn  \fp_set:Nn {Nx}

% #1: input name
% #2: output name
% #3: factor
\cs_set:Npn \__multiply_length:NNn #1#2#3 {
    \fp_set:Nx \l_tmpa_fp {\dim_to_fp:n {#1}}
    \fp_set:Nx \l_tmpb_fp {\l_tmpa_fp * #3}
    \dim_set:Nx \l_tmpa_dim {\fp_to_dim:n {\l_tmpb_fp}}
    \dim_set_eq:NN #2 \l_tmpa_dim
}

Saving and retrieving values in an array list

There are multiple ways to store values into a “list”. In this example, I am using property list to imitate the behavior of array list. One can also use comma-separated list or sequence. It is possible (maybe easier) to use a sequence with \seq_item:Nn to fetch item from a particular index.

\int_new:N \g__aim_counter_int
\int_gset:Nn \g__aim_counter_int {1}
% creat a property list to store and reuse aims
\prop_new:N \g__aim_prop

\cs_generate_variant:Nn \prop_put:Nnn {NVn}

\cs_set:Npn \__add_aim:n #1 {
    \tl_set:Nx \l__tmpa_tl {\int_to_arabic:n {\g__aim_counter_int}}
    %\par this meaning: \cs_meaning:N \l__tmpa_tl
    \prop_gput:NVn {\g__aim_prop} {\l__tmpa_tl} {#1}
    %\par this meaning: \cs_meaning:N \g__aim_prop
    \int_gincr:N {\g__aim_counter_int}
    %\par this meaning: \the\g__aim_counter_int
}


\msg_new:nnn {l3cmd} {keynotfound} {}

\cs_set:Npn \__get_aim:n #1 {
    \prop_get:NnN {\g__aim_prop} {#1} {\l_tmpa_tl}
    \cs_if_eq:NNTF {\l_tmpa_tl} {\q_no_value}
        {
            \msg_set:nnn {l3cmd} {keynotfound} {
                Cannot\ find\ key\ #1\ in\ property\ list.
            }
            \msg_error:nn {l3cmd} {keynotfound}
        }
        {
            \tl_use:N {\l_tmpa_tl}
        }
}

\newcommand{\addaim}[1]{\__add_aim:n {#1}}
\newcommand{\getaim}[1]{\__get_aim:n {#1}}

Outputing factorial

The following code will generate this output:

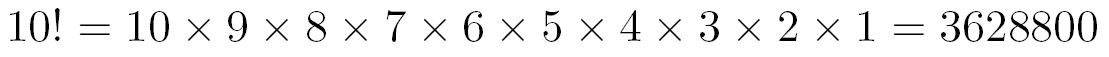
\documentclass{article}
\usepackage{amsmath}
\usepackage{expl3}
\begin{document}
\ExplSyntaxOn
\cs_generate_variant:Nn \int_gset:Nn {Nx}
\cs_set:Npn \print_factorial_helper:n #1 {
    \int_set:Nn \l_tmpa_int {#1}
    \int_compare:nNnTF {#1} {>} {0}
        {% true code
            #1
            \int_compare:nNnTF {#1} {>} {1} {\times} {}
            \int_gset:Nx \g_tmpb_int {\g_tmpb_int * #1}
            \int_decr:N \l_tmpa_int
            \print_factorial_helper:V \l_tmpa_int
        }
        {% false code
            = \int_use:N \g_tmpb_int
        }
}
\cs_generate_variant:Nn \print_factorial_helper:n {V}
\cs_set:Npn \print_factorial:n #1 {
    \int_gset:Nn \g_tmpb_int {1}
    $#1 ! = \print_factorial_helper:n {#1}$
}
\print_factorial:n {10}
\ExplSyntaxOff
\end{document}

Fibonacci numbers

The article on overleaf demonstrates how to print Fibonacci numbers using TeX. The following example shows how to do it in LaTeX3.

\documentclass{article}
\usepackage[T1]{fontenc}
\usepackage{datetime2}
\usepackage{expl3}

\begin{document}
\setlength{\parindent}{0cm}

\ExplSyntaxOn

\int_new:N \g_tmpc_int  % result
\int_new:N \g_tmpd_int  % loop variable

\cs_new:Npn \fibo:n #1 {
    \bool_if:nTF {\int_compare_p:nNn {#1} {=} {1}} {1} {
        \bool_if:nTF {\int_compare_p:nNn {#1} {=} {2}} {1\ 1} {
            1\ 1\ 
            \int_gset:Nn \g_tmpa_int {1}
            \int_gset:Nn \g_tmpb_int {1}
            \int_gset:Nn \g_tmpc_int {0}
            \int_gset:Nn \g_tmpd_int {2}
            \int_do_until:nNnn {\g_tmpd_int} {>} {#1} {
                \exp_args:NNx \int_gset:Nn \g_tmpc_int {\int_eval:n {\g_tmpa_int + \g_tmpb_int}}
                \exp_args:NNx \int_gset:Nn \g_tmpa_int {\g_tmpb_int}
                \exp_args:NNx \int_gset:Nn \g_tmpb_int {\g_tmpc_int}
                \int_use:N \g_tmpc_int\ 
                \int_gincr:N \g_tmpd_int
            }
        }
    }


}

\fibo:n {10}

\ExplSyntaxOff

\DTMNow


\end{document}

The output is as follows:

1 1 2 3 5 8 13 21 34 55 89
2020-06-10 19:37:07-04:00

Integer to roman/roman to integer

This is supported by LaTeX3’s built-in functions:

• \int_to_roman:n
• \int_from_roman:n

Limitations of LaTeX3

• Slow execution speed: most data structures (e.g. sequence, property list) are emulated with native LaTeX commands, which are inefficient.
• Inaccurate and limited floating point support
• Long and meaningless variable names
• The lack of continue and break in loops
• The inability to assign/modify objects in sequences/lists/strings

I am looking into LuaTeX to see if it provides a better combination of an programming language and a typesetter.

Hilighting LaTeX3 Code

One can use the following Lexer in Pygments to highlight LaTeX3 code correctly. A small GUI tool based on this can be found here.

from pygments.lexer import RegexLexer, DelegatingLexer, include, bygroups, \
    using, this, do_insertions, default, words
from pygments.token import Text, Comment, Operator, Keyword, Name, String, \
    Number, Punctuation, Generic, Other


class Tex3Lexer(RegexLexer):
    """
    Lexer for the TeX and LaTeX typesetting languages.
    """

    name = 'TeX'
    aliases = ['tex', 'latex']
    filenames = ['*.tex', '*.aux', '*.toc']
    mimetypes = ['text/x-tex', 'text/x-latex']

    tokens = {
        'general': [
            (r'%.*?\n', Comment),
            (r'[{}]', Name.Builtin),
            (r'[&_^]', Name.Builtin),
        ],
        'root': [
            (r'\\\[', String.Backtick, 'displaymath'),
            (r'\\\(', String, 'inlinemath'),
            (r'\$\$', String.Backtick, 'displaymath'),
            (r'\$', String, 'inlinemath'),
            (r'\\(([glc])_{1,2}[a-zA-Z_@]*)', Name.Variable),
            (r'\\([a-zA-Z_@]+|.)', Keyword, 'command'),
            (r'\\$', Keyword),
            include('general'),
            (r'[^\\$%&_^{}]+', Text),
        ],
        'math': [
            (r'\\([a-zA-Z]+|.)', Name.Variable),
            include('general'),
            (r'[0-9]+', Number),
            (r'[-=!+*/()\[\]]', Operator),
            (r'[^=!+*/()\[\]\\$%&_^{}0-9-]+', Name.Builtin),
        ],
        'inlinemath': [
            (r'\\\)', String, '#pop'),
            (r'\$', String, '#pop'),
            include('math'),
        ],
        'displaymath': [
            (r'\\\]', String, '#pop'),
            (r'\$\$', String, '#pop'),
            (r'\$', Name.Builtin),
            include('math'),
        ],
        'command': [
            (r'\[.*?\]', Name.Attribute),
            (r'\*', Keyword),
            (r':[a-zA-Z]*', Name.Namespace),  # use an unused color
            default('#pop'),
        ]
    }

    def analyse_text(text):
        for start in ("\\documentclass", "\\input", "\\documentstyle",
                      "\\relax"):
            if text[:len(start)] == start:
                return True

Resources

• \expandafter introduction (1)
• \expandafter introduction (2)
• expl3 short intro
• The LaTeX3 Interfaces (Complete manual)
• Creating functions in LaTeX3